1. Расстояние между центрами окружностей радиусов 1 и 9 равно 17. Этих окружностей и их общей внутренней касательной касается третья окружность. Найдите ее радиус.
Решение.
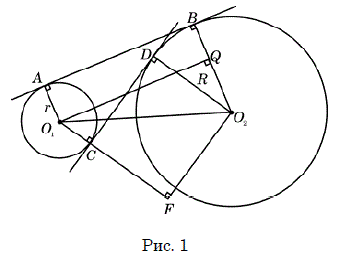 Докажем сначала следующее утверждение. Если – расстояние между центрами
окружностей радиусов r и R
Докажем сначала следующее утверждение. Если – расстояние между центрами
окружностей радиусов r и R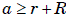 , общая
внешняя касательная касается окружностей в точках A и B общая внутренняя – в точках C
и D, то
, общая
внешняя касательная касается окружностей в точках A и B общая внутренняя – в точках C
и D, то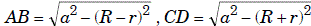 .
. Действительно, пусть
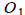 и
и 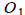 и
и 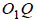 на прямую
на прямую 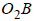 и
и 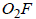 на
прямую
на
прямую 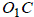 . Из прямоугольных треугольников
. Из прямоугольных треугольников 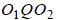 и
и 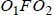 находим, что
находим, что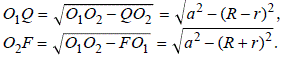
Следовательно,
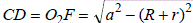 .
.Пусть x – радиус искомой окружности, O – ее центр. Заметим, что прямая CD – либо общая внешняя касательная окружностей с центром O и
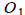 (рис.3). В первом из этих случаев искомая окружность
касается прямой CD в точке C , во
(рис.3). В первом из этих случаев искомая окружность
касается прямой CD в точке C , вовтором – в точке D.
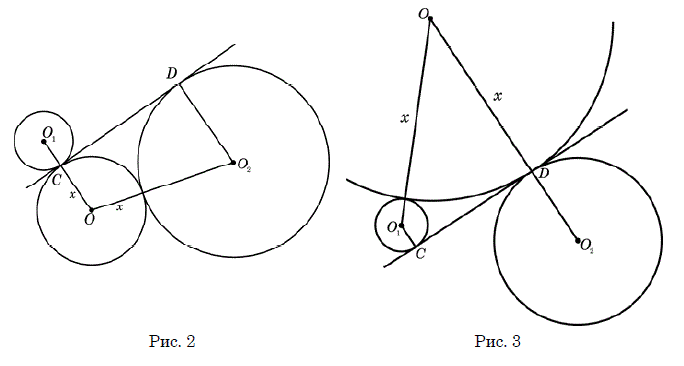
По доказанному 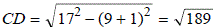 .
.
В первом случае CD – общая внешняя касательная к окружностям с центрами O и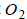 , поэтому
, поэтому 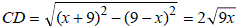 , значит,
, значит,
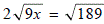 . Следовательно, x
= 24/4.
. Следовательно, x
= 24/4.
Во втором случае CD – общая внешняя касательная к окружностям с центрами O и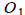 , поэтому
, поэтому 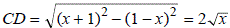 ,
значит,
,
значит, 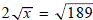 .
.
Следовательно, x = 189/4.
Ответ: 24/4 или 189/4.
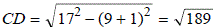 .
.В первом случае CD – общая внешняя касательная к окружностям с центрами O и
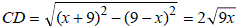 , значит,
, значит,
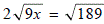 . Следовательно, x
= 24/4.
. Следовательно, x
= 24/4.Во втором случае CD – общая внешняя касательная к окружностям с центрами O и
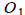 , поэтому
, поэтому 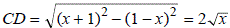 ,
значит,
,
значит, 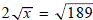 .
.Следовательно, x = 189/4.
Ответ: 24/4 или 189/4.
