1. Найти все значения параметра а, при каждом из которых среди значений функции
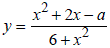
Решение.
1) Функция определена при всех
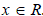. Пусть – одно из значений данной функции. Тогда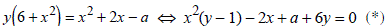
Отсюда следует, что при любом а среди значений функции есть число 1, поскольку при y = 1 для любого существует решение уравнения (*):
.
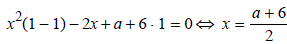2) Пусть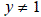
и а – некоторые числа. Тогда уравнение (*) разрешимо относительно x только, если его дискриминант неотрицателен:
.
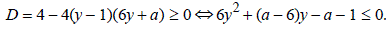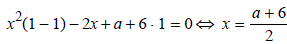.2) Пусть
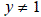и а – некоторые числа. Тогда уравнение (*) разрешимо относительно x только, если его дискриминант неотрицателен: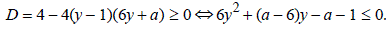.Полученное неравенство при любом а равносильно неравенству
.
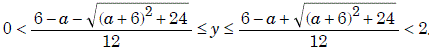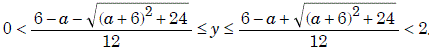.3) Решим систему неравенств:
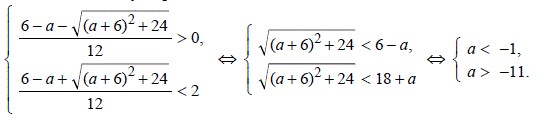
Ответ: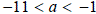
.
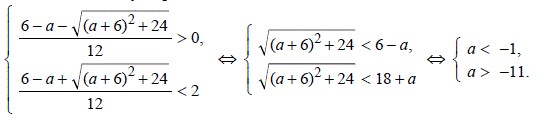
Ответ:
.
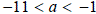